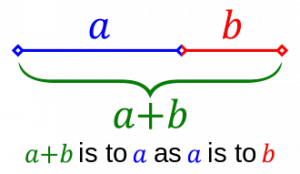
I matematikken er to størrelser i det gyldne snit, hvis deres forhold er det samme som forholdet mellem deres sum og den største af de to størrelser. Figuren til højre illustrerer det geometriske forhold.
Spiraler baseret på Det Gyldne Snit, Fibonacci-spiraler og Gyldne Spiraler optræder ofte i levende organismer. Det gyldne snit findes i geometrien og optræder i grundlæggende konstruktioner af en ligesidet trekant, firkant og femkant placeret inde i en cirkel, såvel som i mere komplekse tredimensionelle faste stoffer som dodekaeder, ikosaeder og Buckyballs.
Der er et særligt forhold mellem det gyldne snit og Fibonacci-tallene (0, 1, 1, 2, 3, 5, 8, 13, 21, … osv., hvert tal er summen af de to tal før det).
Når vi tager to på hinanden følgende Fibonacci-tal, det ene efter det andet, er deres forhold meget tæt på det gyldne snit. Dette kaldes en tilnærmelse eller grænseværdi i kalkulation.
De Golden Ratio-baserede spiraler og Fibonacci-spiralerne bruges i udbredelsen af kunstig intelligens-maskineri og erhverves gennem dannelse af bundne vedhæftninger til den oprindelige Krystal-spiral.
Deres struktur skaber metatroniske kroppe, omvendte Merkaba-forhold og er baseret på konsumerende modellering, som har store konsekvenser for genereringen af falden bevidsthed.
Dette fører til afkobling fra højere dimensionelle forbindelser, skaber bevidsthedsfælder og afskærer væsenet fra udveksling med den evige Gudskilde-strøm.
Phi bruges også som symbol for det gyldne snit og ved andre lejligheder i matematik og videnskab. Denne brug er separat kodet som Unicode-glyffen ϕ.
Fibonacci-sekvensen giver endnu en måde at udlede Phi matematisk på.
Det gyldne snit 1.618033988749894848204586834..optræder i matematik, kunst, natur og arkitektur. Det gyldne snit kaldes også det gyldne middeltal eller det gyldne snit.
Platon (427-347 f.Kr.) beskriver i sin Timaios fem mulige regulære faste stoffer (de platoniske faste stoffer: tetraederet, terningen, oktaederet, dodekaederet og ikosaederet), hvoraf nogle er relateret til det gyldne snit.
Udtrykket “Phi” blev opfundet af den amerikanske matematiker Mark Barr i 1900-tallet. Phi er fortsat med at optræde i matematik og fysik, bl.a. i 1970’ernes Penrose Tiles, som gjorde det muligt at flise overflader i femfoldig symmetri. I 1980’erne dukkede phi op i kvasikrystaller, en dengang nyopdaget form for stof.
Det gyldne snit i renæssancekunsten
Tegningen er baseret på sammenhængen mellem ideelle menneskelige proportioner og geometri, som den gamle romerske arkitekt Vitruvius beskrev i bog III i sin afhandling De Architectura.
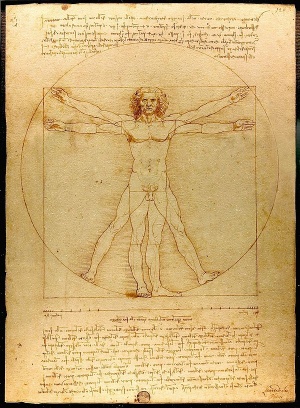
I 1509 skrev Luca Pacioli en bog, der refererer til tallet som den “Guddommelige Proportion”, som blev illustreret af Leonardo da Vinci. Da Vinci kaldte det senere sectio aurea eller det gyldne snit. Det gyldne snit blev brugt til at opnå balance og skønhed i mange af renæssancens malerier og skulpturer. Da Vinci brugte selv det gyldne snit til at definere alle proportionerne i sin sidste nadver, herunder bordets dimensioner og proportionerne på væggene og baggrunden. Det gyldne snit optræder også i da Vincis vitruvianske mand og Mona Lisa. Andre kunstnere, der har anvendt det gyldne snit, er Michelangelo, Raphael, Rembrandt, Seurat og Salvador Dali.
Den vitruvianske mand er en tegning af Leonardo da Vinci fra omkring 1490. Den er ledsaget af noter baseret på arkitekten Vitruvius’ arbejde. Tegningen, som er lavet med pen og blæk på papir, forestiller en mand i to overlejrede positioner med arme og ben adskilt og indskrevet i en cirkel og en firkant. Tegningen og teksten kaldes undertiden Proportionernes kanon eller, mindre ofte, Menneskets proportioner.
Det gyldne snit i naturen
Det gyldne snit optræder også i alle former for natur og videnskab.
Nogle steder kan nævnes:
- Blomsterblade: Antallet af kronblade på nogle blomster følger Fibonacci-sekvensen.
- Frøhoveder: Frøene i en blomst produceres ofte i midten og vandrer udad for at fylde rummet. For eksempel følger solsikker dette mønster.
- Fyrrekogler: Spiralmønsteret i frøkapslerne snor sig opad i modsatte retninger. Antallet af trin, spiralerne tager, har tendens til at matche Fibonacci-tal.
- Solsikkefrø: Solsikkefrø vokser i Fibonacci-spiraler.
- Trægrene: Den måde, trægrene dannes eller deler sig på, er et eksempel på Fibonacci-sekvensen. Rodsystemer og alger udviser dette dannelsesmønster.
- Skaller: Mange skaller, herunder sneglehuse og nautilusskaller, er perfekte eksempler på den gyldne spiral.
- Spiralgalakser: Mælkevejen har en række spiralarme, som hver har en logaritmisk spiral på ca. 12 grader. Spiralens form er identisk med den gyldne spiral, og det gyldne rektangel kan tegnes over enhver spiralgalakse.
- Orkaner: Ligesom skaller viser orkaner ofte den gyldne spiral.
- Fingre: Længden af vores fingre, hver sektion fra spidsen af basen til håndleddet, er større end den foregående med omtrent forholdet Phi.
- Dyrekroppe: Målingen af den menneskelige navle til gulvet og toppen af hovedet til navlen er det gyldne snit. Men vi er ikke de eneste eksempler på det gyldne snit i dyreriget; delfiner, søstjerner, sanddollars, søpindsvin, myrer og honningbier udviser også proportionen.
- DNA-molekyler: Et DNA-molekyle måler 34 Ångström x 21 Ångström ved hver fuld cyklus af dobbeltspiralen. I Fibonacci-serien er 34 og 21 på hinanden følgende tal.
Fibonacci-spiralen
Fibonacci-spiralen kommer tættere og tættere på en gylden spiral, efterhånden som den vokser i størrelse på grund af forholdet mellem hvert tal i Fibonacci-serien og tallet før det, der konvergerer mod Phi, 1,618, efterhånden som serien skrider frem.
Den begynder med nul, derefter 1, og går så videre til det næste tal, således: 0+1=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8 og så videre.
Når vi anvender denne matematiske formel til at kvantificere eller måle bevægelsen af energi eller bevidsthed i tid eller rum, mister Fibonacci-spiralen sin forbindelse tilbage til nulpunktet eller kilden, i stedet bruger sekvensen det foregående tal til at lægge til sig selv for at komme til det næste højere tal i sekvensen. Den har ingen forbindelse til midten, så den knytter sig til en anden eller fortærer det, der er på dens vej for at ekspandere. Fibonacci-spiraler illustrerer den matematik, der bruges til at opretholde krigen om energi og dermed bevidsthedsundertrykkelsen på jorden. Når sekvensen vokser i antal eller størrelse, skyldes det forbruget af de tidligere værdier for at vokse sig større.
Jo større den bliver, jo mere forbruger den, og den bevæger sig gradvist ud og væk fra den organiske krystalspiral i det oprindelige kernemanifestationslegeme eller guddommelige skabelonlegeme, efterhånden som den ekspanderer. (Se forbrugende modellering).
Derfor er Fibonacci-spiralen en matematisk model for metatronisk reversering, der er registreret i bevidsthedsfelterne, der i sidste ende knytter sig som en parasit til en levende vært og samler affaldsprodukter, såsom akkumulerende giftige Miasma-felter, der dannes til Qlippoth eller Adverse Sephiroth, i Phantom Matrix for at inficere det universelle livstræ.
Gylden spiral
I geometrien er en gylden spiral en logaritmisk spiral, hvis vækstfaktor er φ, det gyldne snit. Det vil sige, at en gylden spiral bliver bredere (eller længere væk fra sit udspring) med en faktor på φ 1,618 for hver kvart omdrejning, den foretager. Da forholdet mellem på hinanden følgende Fibonacci-tal nærmer sig det gyldne snit, når Fibonacci-tallene nærmer sig uendeligt, bliver denne gyldne spiral også mere lig den tidligere tilnærmelse, jo flere firkanter der tilføjes.
Krystal-spiralen
Forskellene mellem Krystalspiralen og Fibonacci-spiralen og det gyldne snit Fibonacci-spiralen og -sekvensen kan forstås ud fra deres respektive forhold til deres skabelsespunkt. Krystalspiralen og den matematiske sekvens, som den udspringer af, kommer direkte fra nulpunktet eller det centrale punkt for al forening.
Krystalspiralen bevarer hele tiden en levende, åndende forbindelse gennem bevarelsen af det, der kom før, mens den udvider sig gennem multiplikation.
